MACLEAN’S ARITHMETIC AND ITS EFFECT

ON UNIVERSITIES’ RANKINGS

Doug Shale

Yolanda Liu

Office of Institutional Analysis

University of Calgary

2500 University Drive N.W.

Calgary, Alberta T2N 1N4

http://www.oia.ucalgary.ca/

Paper presented at the Annual Conference of the Canadian Institutional Research

and Planning Association; Ottawa, Ontario; October 6-8, 2002.

MACLEAN’S ARITHMETIC AND ITS EFFECT ON UNIVERSITIES’ RANKINGS

Doug Shale

Yolanda Liu

University of Calgary

Abstract

It has been acknowledged for some time that the Maclean’s ranking methodology can amplify small reported differences in raw data submitted by the institutions being ranked. The conversion of interval-level, raw data to ordinal-level ranks is partially responsible for transforming minor and variable differences in raw data to the apparent equal differences in ranking values. However, there is yet another dynamic that, of itself, also produces distortions. This is the particular arithmetic used by Maclean’s to convert raw data on each indicator to points on each indicator which, when summed over all indicators, results in an overall score for each university (which, in turn, is the basis for the overall rankings). This paper will show how the Maclean’s statistical methodology causes distortions in the scaling of data and will assess the consequences of this distortion by recalculating the points and rankings by alternative, equally “valid” approaches.

Introduction

The Maclean’s ranking exercise has been criticized from a number of points of view (see, for example, Page, 1995; 1996). The most fundamental level of criticism has to do with the philosophical basis of the rankings. What does it mean to claim that a given university is number 1, another number 2 and so on? What does “quality” mean with respect to universities and can it truly be measured? Is there a justification for the Maclean’s view that there are recognized and accepted proxies for quality and that relative values can be assigned to these proxies – and that a summation of these values legitimately represents an overall measure of relative quality?

The Maclean’s ranking exercise has also been criticized because the values resulting from of the indicators used and the associated rankings are often unpredictably variable – which, taken together with other information, would indicate that the data reported are to some indeterminate extent invalid (Wilson, 1999). In any event, the question of data validity is open since there are no satisfactory audit procedures in place to ensure adherence to the reporting protocols.

In addition to the argument about whether it makes sense to definitively rank universities, there has also been criticism of the use of rankings because small differences in raw score values can be amplified when converted to a rank. So, for example, the difference in a placement of one rank position could be the result OF very small difference (potentially, even by a single decimal point) – but that difference would appear to be the same as a one ranking difference where one raw score value was substantially larger or smaller than another.

However, there is yet another factor that causes a “disproportioning” of raw score differences – and this is due to the particular (and unusual) arithmetic that Maclean’s uses to calculate the indicator sub-scores and the overall scores on which the overall rankings are based.

Maclean’s transforms the raw data for each university on each indicator using what they call a “statistical percentile rank” method. The starting point is the matrix of all the Maclean’s indicator values for all of the universities in the given group (as presently published in the Maclean’s rankings issue). Each of the 3 Maclean’s groupings of universities has its own matrix. A mean value and standard deviation are calculated for each indicator. Each indicator score for each university is converted to a z-score value by taking the particular indicator raw value for each university, subtracting the indicator mean value and dividing by the standard deviation for that indicator. Each z-score value is then referred to the Standard Normal distribution (or Normal curve, as it is commonly known). The z-score value is converted to the corresponding cumulative probability (also called the area under the Normal curve). Under the assumptions associated with the normal distribution, the “area under the curve” can be interpreted as a percentile rank score – so, for example, if the cumulative probability is .7500, the given score is deemed to be larger than 75 percent of all of the scores.

Maclean’s then multiplies this percentile value by the weighting factor assigned to that indicator. The result is some number of points corresponding to the raw score value of the indicator for the given university. These points are obviously not necessary to determine the ranking of each institution on each indicator because we could get that directly from the raw scores. However, we do need some way to transform the raw scores to the equivalent in points (out of the assigned weighted amount) so that the sub-scores can be added to provide us with an overall points total - which then converts to an overall ranking.

A property of the Normal curve is that it is asymptotic. Each end of the curve approaches the X-axis but, in mathematical terms, never meets the axis. A consequence of this for the Maclean’s rankings is that, for all intents and purposes, it is not possible to obtain the full number of points allocated to any of the indicators. It follows, then, that although 100 points are allocated in the assigned weightings, the first ranked institution will never achieve 100 points. A further peculiarity of the Maclean’s calculus is that a change in the raw value of any specific indicator will affect the points earned by all the universities on that indicator. The reason for this is that a change in any one score changes the mean value and standard deviation of the indicator – and that, of course, changes the corresponding z-scores, which changes the percentile scores and so on.

What is not widely appreciated is that the Maclean’s approach of referencing the normal curve causes a “disproportioning” in the awarding of points. This is because a property of the Normal curve is that the percentile values for a constant difference in z-score value are smaller the farther out one goes in the tails of the distribution. To put it another way, the difference in percentile value between z-scores of, say, 3.0 and 3.1 is smaller than the percentile value between z-scores of 1.0 and 1.1 even though the difference in the z-scores is 0.1 in both cases. In turn this means that a high achieving institution receives fewer points because the percentile rank multiplier will be smaller because of where it places on the curve. Similarly, a low achieving institution will achieve fewer points because it is at the spread-out, lower end of the normal curve.

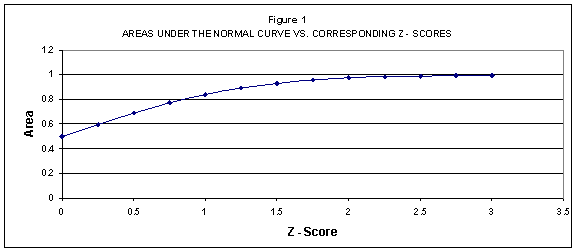
Figure 1 shows this phenomenon by plotting z-scores against the corresponding cumulative probability values. If the area under the curve was a constant amount for the given difference in z-scores, the graph should be a straight line. In actuality, the line curves, indicating that the ‘area-under-the-curve’ differences are not constant.

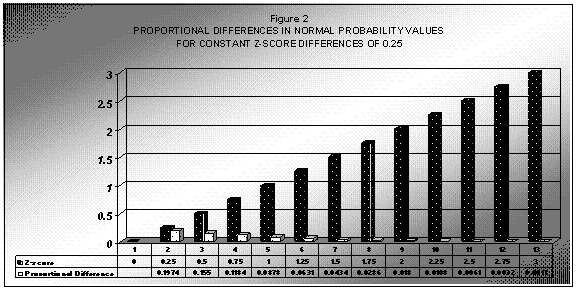
Another view of this that makes the variable relationship more obvious is to plot the proportional differences in the Normal probability values against constant differences in z-score values. This is presented in Figure 2. Constant increases of .25 in z-score values result in decreasing “area under the Normal curve” values.

Given these mathematical peculiarities associated with Maclean’s referencing the Normal probability distribution does this choice of arithmetic methodology make a material difference to the rankings? If it does, we have yet one more basis for questioning the validity of the Maclean’s rankings.

Alternative Scoring Procedures

We can address the question of whether the Maclean’s arithmetic, of itself, affects the rankings by asking what other arithmetic approaches could be used instead - and to what effect. We have one possibility immediately at hand – and that is the calculus used by the U.S. News & World Report.

Another possibility is to calculate the simple proportionate differences in raw scores and apply these to the allocated of weights.

If we use a scoring procedure based on proportionate differences, what might we use as an index value – that is, what should we use as the base for determining proportionate differences? There are two obvious candidates. One is a variation of the normalization approach used in the US News & World Report approach where the top score becomes indexed at 1 and all other scores are proportioned by dividing each score by the highest score. The variation would be that we would use the actual values for each indicator over all universities rather than the aggregate score over all indicators for all universities.

A second possibility is to index all raw score values to the mean value of each indicator. We would expect to see some difference depending on whether the highest value or average value is used as the index if only because the mean value approach would buffer the effects of widely dispersed scores – whereas the highest value approach would tend to optimize the effect of such a distribution of scores.

In any event, all 4 of these approaches begin with a matrix of data gathered by Maclean’s (much of this data is obtained through a survey sent to the universities; data for two indicators are derived from Statistics Canada data; the Reputation data is obtained by means of a survey sent to various of university officials, CEOs and recruiters, heads of national and regional organizations, and high school counselors). The matrix is comprised of a listing of the universities along one dimension and an enumeration of each of the Maclean’s indicators along a second dimension. Maclean’s categorises the universities into 3 separate groupings: the Primarily Undergraduate institutions, the Comprehensive institutions, and the Medical/ Doctoral universities. There is a matrix of data for each of the 3 groupings (note that in addition to the obvious differences of which universities are in which category, there may also be differences in the indicators applied to each category and in the relative weightings assigned).

Details showing the ranking factors, indicators and associated weightings for the 3 categories of universities are given in Figure 3.

Figure 3 MACLEAN'S RANKING FACTORS, INDICATORS AND WEIGHTS (as of 2001)
Ranking Category	Med/Doc & Comp.	Undergrad	Subfactor		Med/Doc	Comp.	Undergrad
			Avg. entering grade		11%	11%	11%
			Proportion with 75% or high		3%	3%	3%
Student body	22%	21%	Proportion who graduate		2%	2%	2%
			Out of province (1st-year)		1.5%	1.5%	1.5%
			International (1st-year)		0.5%	0.5%	0.5%
			International (graduate)		1%	1%	N/A
			Student awards		3%	3%	3%
			Class size (1st & 2nd year)		7%	7%	7.5%
Classes	17%	18%	Class size (3rd & 4th year)		7%	7%	7.5%
			Classes taught by tenured faculty		3%	3%	3%
			Faculty with PhDs		3%	3%	3%
Faculty	17%	17%	Awards per full-time faculty		3%	3%	3%
				Avg. grant size per faculty	2.75%	2.75%	2.75%
			Social Sciences & Humanities Grants	Number of grant per faculty	2.75%	2.75%	2.75%
				Avg grant size per faculty	2.75%	2.75%	2.75%
			Medical/Science Grants	Number of grant per faculty	2.75%	2.75%	2.75%
			Operating budget		3.33%	3.33%	3.33%
Finance	12%	12%	Scholarship & Bursaries (percentage of budget)		4.33%	4.33%	4.33%
			Student services (Percentage of budget)		4.33%	4.33%	4.33%
			Total holdings		1%	N/A	N/A
			Holdings per student		3%	4%	4%
Library	12%	12%	Acquisitions		4%	4%	4%
			Expenditures		4%	4%	4%
			Alumni support		5%	5%	5%
Reputation	20%	20%	Reputational survey		15%	15%	15%
Total	100%	100%	-		100%	100%	100%

For the purposes of this paper, we will only consider the Medical/ Doctoral group of universities and their associated data matrix. All of the calculations presented here are based on the data published in the November 19, 2001 edition of Maclean’s magazine – although there is one proviso. Maclean’s does not publish the data from the Reputational survey. We could re-calculate the rankings using only the other indicators. However, the reputation scores do make a significant difference to some universities’ rankings. We are able to estimate the Reputation scores, however, and it seems preferable to us to work with rankings that correspond to what is published in the November 19, 2001 issue of Maclean’s (the estimation process involves assigning Reputation scores to each university such that the over-all ranking without consideration of the reputation scores is transformed to the over-all ranking as published).

We have not presented this data matrix here because of the amount of detail involved. However, the data set is available from the authors (as are the data sets for the other two groupings not re-analysed here).

We have already described the calculation used by Maclean’s – although we should, perhaps, add that there are also two “behind the scenes” subsidiary calculations that Maclean’s performs to produce the indicator values that we actually see published in the magazine. One of these concerns the class size indicator and the other is the calculation of weighted FTE used in the “Operating Budget per Student” indicator. Neither of these additional calculations is germane for the purposes of this paper, so we will not go into them here. However, details in this regard are available in Shale and Liu (2002).

We have also described the indexing approaches of using the highest raw score and average of the raw scores for each indicator – and assigning proportionate scores accordingly. These normalized scores are then multiplied by the weight designated for the corresponding indicator and summed to yield an over-all score which provides the basis for determining the over-all rankings.

The approach taken by U.S. News & World Report is a blend of the Maclean’s method and the indexing approach. U.S. News also begins by calculating a mean and standard deviation from the raw score values on each indicator – and converts each raw score on that indicator to a z-score value (by subtracting the indicator mean from each individual raw score and dividing by the standard deviation). However, unlike Maclean’s, U.S. News does not reference the Normal distribution. Instead the z-score values are all re-scaled by subtracting the smallest z-score value from all the z-score values for the given indicator. This makes all of the z-scores positive. These re-scaled, positive z-scores are then multiplied by the weight assigned for the particular indicator – and the product represents the point totals for each university on that indicator. This is repeated over all indicators. The resulting points are totaled to yield an over-all total score for each university. (These totals are then normalized by dividing the largest total into each of the over-all totals; the highest scoring institution is awarded a normalized score of 100. This normalization, of course, is not necessary to determine the rankings.)

The Results

Table 1 displays the points totals calculated through the 4 approaches described above.

Table 1 POINTS TOTALS FOR MEDICAL/DOCTORAL UNIVERSITIES^1 USING 4 DIFFERENT ARITHMETIC METHODS
	Maclean's	U.S. News	Highest Score	Average Score
Toronto	79.2	285.51	93.43	126.42
Queen's	71.02	245.14	84.44	112.87
McGill	67.53	237.66	85.8	117.39
UBC	73.43	259.59	87.27	117.71
McMaster	44.22	156.11	74.81	97.91
Dalhousie	43.64	165.71	72.37	95.02
Western	58.17	208.56	78.91	103.28
Alberta	59.88	212.49	81.98	109.15
Ottawa	43.45	167.32	74.12	97.52
Saskatch.	37.13	135.95	64.87	81.67
Sherbrooke	27.51	106.58	63.12	78.85
Montreal	55.96	199.86	75.96	99.98
Laval	33.95	126.35	69.55	90.29
Manitoba	19.73	73.5	61.58	78.17
Calgary	33.95	132.13	70.33	93.27
1. Based on data reported in Maclean's magazine, November 19, 2001.

How similar and dissimilar are the points totals derived from the 4 arithmetic methods? Inspection of Table 1 provides us with a rough sense of an answer to this question. However, a more rigorous way to determine the extent to which similarities and differences exist is to correlate the scores. The result of doing so is displayed in Table 2.

Table 2 CORRELATIONS^1OF POINTS TOTALS RESULTING FROM THE 4 ARITHMETIC METHODS
	Maclean's	U.S. News	Highest Score	Average Score
Maclean's	1
U.S. News	0.9972	1
Highest Score	0.9740	0.9767	1
Average Score	0.9641	0.9675	0.9976	1
1. Correlations are based on the points totals listed in Table 1.

All 4 methods seem to agree quite well judging by the magnitude of the correlation coefficients. The highest level of agreement is between the highest score and average score methods. The lowest level of agreement is between the Maclean’s approach and the average score method.

With such high correlations among the total scores obtained from the 4 methods can we conclude that it essentially doesn’t matter which method we use? Another view of the situation is to examine the rankings that are derived from the total scores of the 4 methods. Small differences in raw scores can translate into a substantive difference in the associated rankings and, indeed, that occurs here. Table 3 shows the rankings that are obtained from the total scores given in Table 1.

Table 3 SUMMARY OF RANKINGS CALCULATIONS^1
	Maclean's Rank	US News Rank	Highest Score Rank	Average Score Rank
Toronto	1	1	1	1
Queen's	3	3	4	4
McGill	4	4	3	3
UBC	2	2	2	2
McMaster	8	10	8	8
Dalhousie	9	9	10	10
Western	6	6	6	6
Alberta	5	5	5	5
Ottawa	10	8	9	9
Saskatch.	11	11	13	13
Sherbrooke	14	14	14	14
Montreal	7	7	7	7
Laval	12	13	12	12
Manitoba	15	15	15	15
Calgary	12	12	11	11
1. Data for the Medical/Doctoral groups as published by Maclean's, November 19, 2001.

The Maclean’s rankings, of course, correspond to what was published in the November 19, 2001 edition of their magazine.

In 8 instances, the rankings of the specific universities involved are the same whichever method of calculation we use. These are Toronto (with a ranking of 1), UBC (with a ranking of 2), Alberta (at 5^th), Western (6^th), Montreal (7^th), Sherbrooke (14^th), and Manitoba (15^th). In the other 7 instances, there was a difference of at least one position resulting from at least one of the methods of calculation – and in some cases, there is a difference of 2.

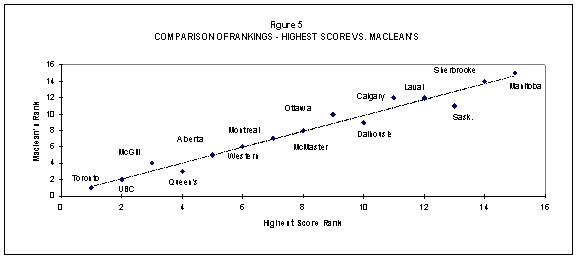
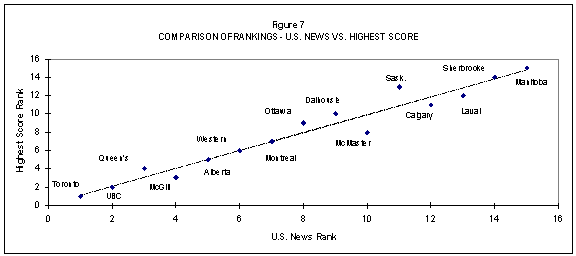
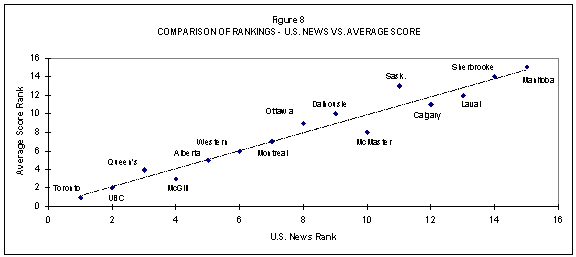
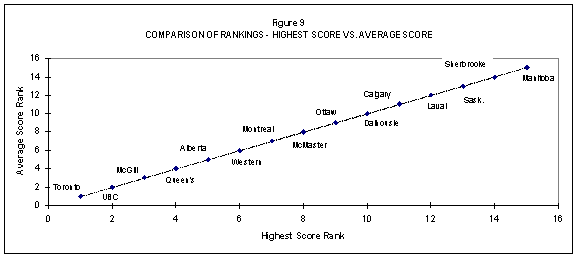
Figures 4 to 9 compare the rankings method by method, which makes more apparent where similarities and differences exist. The figures also better indicate visually where there are differences and how pronounced they are.

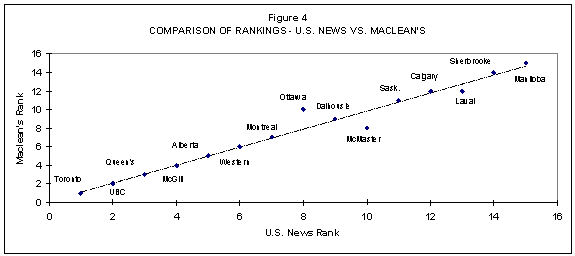
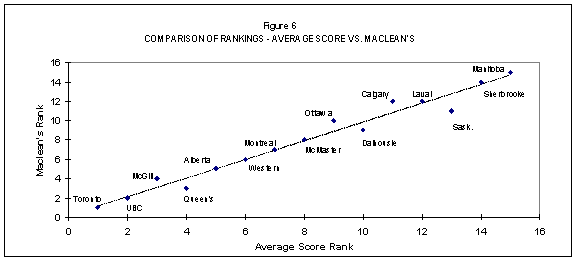
Perhaps the most interesting comparison is between the method of calculation used by Maclean’s and by the U.S. News & World Report. These, of course, are the two notable published university rankings. As Shale and Liu (2002) have indicated, there are more differences than similarities between the approaches taken by each magazine. However, it is striking that, all other things being kept constant, the rankings produced by each are affected by the arithmetic each has used. Since the differences in arithmetic have no apparent rational basis, we would conclude that the effect on the final rankings is spurious. However, when these rankings are published they are represented as something absolute and meaningful.

There are perturbations apparent in each of Figures 5 to 8 and, again, these do vary according to the arithmetic used. Figure 9 is especially interesting because of the degree of concordance apparent between the two approaches taken to normalizing the raw scores on the indicator. The line of best fit effectively passes through all the data pairs.

Implications and Conclusions

The Maclean’s method for calculating ranks is very complex and involved and not intuitively understandable. This cloaks the rankings themselves in more mystery than need exist. Moreover, Maclean’s claims, implicitly and explicitly, to be measuring the quality of universities to an extent that allows them to state without qualification that one institution is number one, another number two and so on to the very last. If this rank ordering is affected by the simple choice of arithmetic used to convert raw data to points, what does that have to say about the validity of Maclean’s claims to have the “true” measure of quality?

Hopefully, a more public review of the heretofore “hidden” side to the calculations of the Maclean’s rankings will also provide some incentive for Maclean’s to become more transparent in all aspects of its rankings process.

References

America’s Best Colleges; 2002 Edition; U.S. News & World Report; Washington, D.C.

Clarke, Marguerite “Quantifying quality: What can the U.S. News and World Report rankings tell us about the quality of higher education?”; Education Policy Analysis Archives; Volume 10, Number 16; March 20, 2002; http://epaa.asu.edu/epaa/v10n16/.

Lawrence, Judith K. and Green, Kenneth C. A Question of Quality: The Higher Education Ratings Game; ASHE/ ERIC Higher Education Report; Number 5; 1980.

Mallet, Bruce I. “Money Magazine, U.S. News & World Report, and Steve Martin: What Do They Have in Common?” In R. Dan Walleri and Marsha K. Moss (Editors) Evaluating and Responding to College Guidebooks and Rankings; New Directions for Institutional Research; Number 88, Winter 1995; Jossey-Bass Publishers; San Francisco; pp 31-43.

McGuire, Michael D. ‘ “How insensitive can you get?” Further analysis of the Best Colleges rankings.’ Paper presented at the 20^th Annual Conference of the Northeastern Association for Institutional Research; Bolton Landing, New York; November 6-9, 1993.

McGuire, Michael D. “Validity Issues for Reputational Studies”; In R. Dan Walleri and Marsha K. Moss (Editors) Evaluating and Responding to College Guidebooks and Rankings; New Directions for Institutional Research; Number 88, Winter 1995; Jossey-Bass Publishers; San Francisco.

Morse, Robert J. “U.S. News &World Report’s College Rankings”. Paper presentation at Association for Institutional Research Annual Forum; :Long Beach, California; June 3-6, 2001.

Morse, Robert J. and Flanigan, Samuel “How we rank colleges”. http://www.usnews.com/usnews/edu/college/rankings/about/02cbrank.htm

Page, Stewart “Rankings of Canadian Universities: Pitfalls in Interpretation”. The Canadian Journal of Higher Education; Vol. XXV-2, 1995; pp 17 – 28.

Page, Stewart “Rankings of Canadian Universities, 1995: More Problems in Interpretation”; The Canadian Journal of Higher Education; XXVI – 2; 1996; pp 47-57.

Schultz, R. “Maclean’s rankings, a decade later …”. Paper presented at the 10^th Annual Conference of the Canadian Institutional Research and Planning Association; Victoria, British Columbia; October 28 – 31, 2001.

Shale, Doug and Liu, Yolanda “Ranking the Rankers of Universities: Canada’s Maclean’s Magazine vs U.S. News & World Report.” Paper presented at the Forty-second Annual Forum of the Association for Institutional Research; June 2-5, 2002; Toronto, Ontario, Canada.

Stuart, Debra L. “Reputational Rankings: Background and Development”; In R. Dan Walleri and Marsha K. Moss (Editors) Evaluating and Responding to College Guidebooks and Rankings; New Directions for Institutional Research; Number 88, Winter 1995; Jossey-Bass Publishers; San Francisco.

Walleri, R. Dan and Moss, Marsha K. (Editors) Evaluating and Responding to College Guidebooks and Rankings; New Directions for Institutional Research; Number 88, Winter 1995; Jossey-Bass Publishers; San Francisco.

Wilson, Paul “Damn Yankees: An Analysis of Change and Stability in the Maclean’s Rankings of Canadian Universities”. Paper presented at the 8th Annual Conference of the Canadian Institutional Research and Planning Association; Quebec City; October 24-26; 1999.